GRAYŮV KÓD (vícestopý, absolutní)

Binary Reflected Gray Code (BRGC)

Charakteristika

Grayův kód (podle autora Franka Graye), patří do skupiny bezpečných kódů, tedy zajišťuje jednoznačnost informace tím, že při přechodu z jednoho stavu do druhého se mění stav informace pouze v jednom bitu (podobně i Johnsonův kód). Konstrukce kódu je nazývána jako uzavřená a zrcadlová (n-1 stop nebo bitů jsou shodné v opačném pořadí) a taktéž umožňuje detekci chyb i samoopravné funkce.

Použití

Snímače polohy

Praktické využití kódu spadá do oblasti technologií, kde je potřeba zajistit jednoznačnost informace. Prvotní užití bylo určeno pro zamezení čtení chybného stavu elektromechanických nebo optických (nejen) absolutních snímačů polohy jak lineárních tak rotačních.

Digitální komunikace

Pro svoji univerzálnost použití a jednoduché kódování a dekódování při použití výpočetní techniky (kaskádní XOR) našel uplatnění i v oblasti digitální komunikace (např. pozemní digitální a kabelová televize).

Logické hlavolamy

Pro řešení kaskádních hlavolamů jako je Hanojská věž, Čínské kroužky.

Karnaughova mapa

Kód je používán pro popis stavu os mapy.

Komunikace mezi doménami

Zjednodušeně se jedná o specielní případ zajištění synchronizace a zamezení stavu ztráty přenosu informace mezi číslicovými jednotkami pracujících na různých frekvencích.

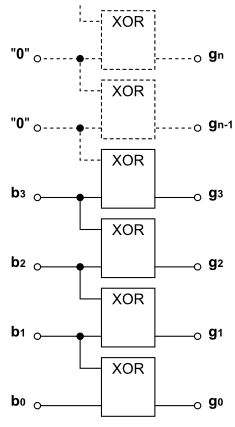
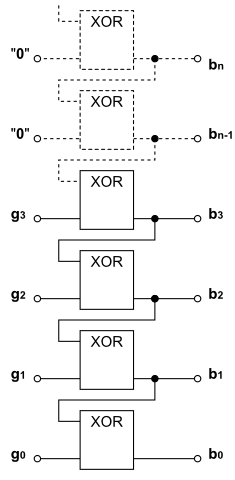
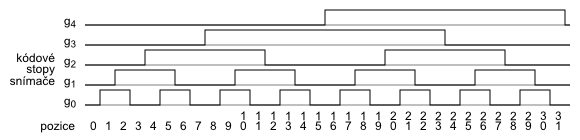
Vyjádření Grayova kódu

Vyjádření Grayova kódu vychází z podmínky, že při změně stavu (z aktuálního do následujícího stavu) je povolena (přípustná) změna stavu pouze v jedné stopě (bitu) kódového slova.

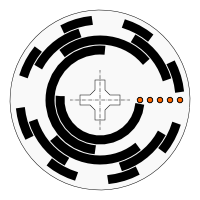
Grayův kód je na rozdíl od mechanického Johnsonova kódu variabilní a přímo neurčuje, jaké je pořadí změn hodnot v jednotlivých stopách (bitech) kódu. Pro vysvětlení toho problému využijeme model hyperkostky, viz obrázek 1, pro tři stopy (bity), kdy jednotlivým vrcholům přiřadíme konkrétní možné stavy a to tak, že sousední vrcholy se liší změnou hodnoty pouze na jedné pozici a protilehlé vrcholy jsou vzájemně komplementní. Pro správnou funkci platí, že pohyb z jednoho stavu do druhého je možný pouze po hranách kostky.

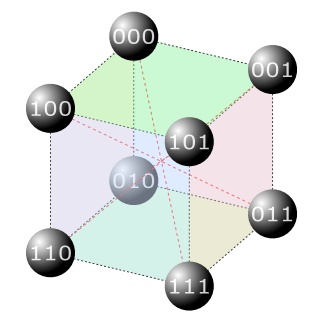
Obrázek 1
Hyperkostka pro tři stopy Grayova kódu, taktéž Karnaughova mapa

Reálně je možno projít všechny vrcholy kostky tak, aby žádný z vrcholů nebyl navštíven dvakrát, což je další nutnou podmínkou. Této vlastnosti se říká, že je splněna Hamiltonovská kružnice (Hamiltonovský graf). V opačném případě by nastala nejednoznačnost kódu.

Z praktického hlediska je zřejmé, že z vrcholu (stavu) 000 do vrcholu (stavu) 111 a zpět je možno se dostat několika cestami. Z vrcholu 000 je možno se vydat libovolným směrem, tedy 3 možnosti, protože je vždy splněna podmínka, že ke změně může dojít pouze v jedné stopě, tedy 000 => 100 nebo 000 => 010 nebo 000 => 001. Obdobně se postupuje při volbě cesty do dalšího nenavštíveného bodu ale tyto možnosti jsou již pouze 2, protože se nevracíme zpět. 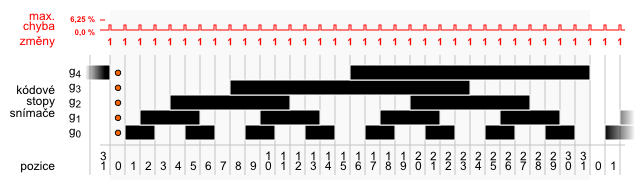Tímto se postupně eliminuje počet zbývajících vrcholů, kterými je nutno projít. Na obrázku 2 jsou zobrazeny příklady postupného průchodu jednotlivými vrcholy (stavy). Je zde však zobrazena pouze polovina možných variant průchodu, protože druhá polovina je reverzní ke směru pohybu.

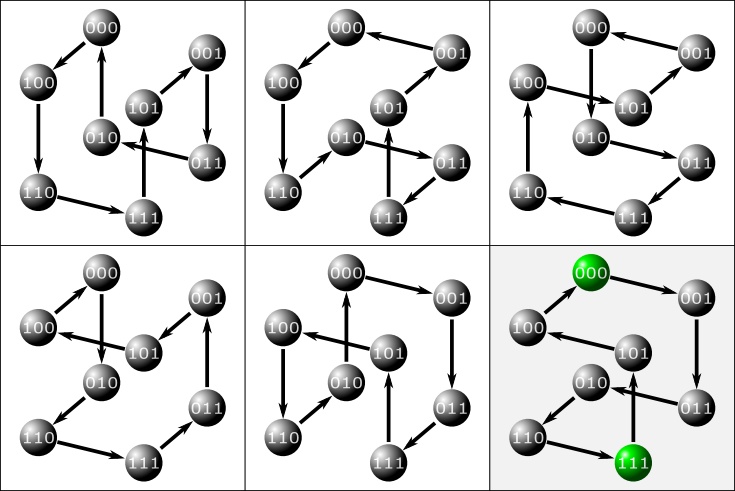
Obrázek 2
Příklady průchodu jednotlivými stavy.

Poslední (zvýrazněný) obrázek ukazuje případ, který je prakticky používán a nejvíce se přibližuje klasickému kódování ve dvojkové soustavě, viz pro porovnání tabulka 1.

Z praktického hlediska je zřejmé, že pouhé 3 stopy pro praktické využití jsou nedostatečné (nízké rozlišení, málo kombinací), na následujícím obrázku 3 je zobrazena konstrukce hyperkostky pro 4 stopy v další (vnější vrstvě), s dvojnásobným počtem možných stavů. S každou další vrstvou (rozměrem) se pak počet možných kombinací zdvojnásobí, obdobně jako u dvojkové-binární soustavy.

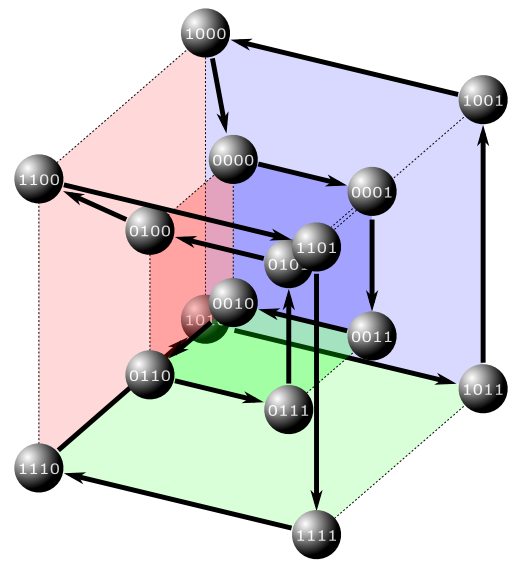
Obrázek 3
Hyperkostka pro 4 stopy Grayova kódu, taktéž Karnaughova mapa

Zpracování Grayova kódu

Grayův kód je možno generovat a dekódovat jednoduchým způsobem pomocí logické funkce XOR jak v řídících systémech PLC, v klasických PC tak i hardwarově.

Generování Grayova kódu

Tabulka 1 zobrazuje převod mezi desítkovou a dvojkovou soustavou a generování Grayova kódu.

Generování Grayova kódu při použití logických členů XOR je vhodné pro program PLC nebo hardwarové řešení, jak ukazuje obrázek 4. Podle tohoto obrázku je možno jednoduše sestavit programový algoritmus pro libovolný počet stop (bitů) Grayova kódu.

Obrázek 4
Generování Grayova kódu z binární soustavy pro 4 stopy.

Dekódování Grayova kódu

Tabulka 2 zobrazuje dekódování Grayova kódu do dvojkové soustavy a odpovídající vyjádření v soustavě desítkové. Dekódování je mírně složitější, hodnota aktuálního bitu je závislá na hodnotě bitu vyššího a pro je nutno vždy postupovat od vyšších stop (bitů) k nižším.

Dekódování Grayova kódu při použití logických členů XOR je vhodné pro program PLC nebo hardwarové řešení, jak ukazuje obrázek 5. Podle tohoto obrázku je možno jednoduše sestavit programový algoritmus pro libovolný počet stop (bitů) Grayova kódu.

Obrázek 5
Dekódování Grayova kódu do binárního soustavy pro 4 stopy.

Absolutní snímače s Grayovým kódem

V kapitole o dvojkové soustavě je uveden příklad technologické nedostatečnosti této soustavy pro technologické aplikace, tuto nedostatečnost eliminuje použití Grayova kódu v této oblasti.

Pro technologické aplikace s požadavkem na jednoznačnost určení stavu, konkrétně polohy, se používá Grayový kód o potřebné počtu stop (bitů) podle požadovaného rozlišení u rotačních snímačů polohy (obrázek 6) nebo délkových - lineárních snímačů polohy (obrázek 7). Snímače jsou nazývány absolutní proto, že vždy poskytují konkrétní informaci o poloze.

Obrázek 6
Rotační kotouč s Grayovým kódem (5 stop)

Obrázek 7
Pravítko s Grayovým kódem (5 stop)

Z praktického hlediska je zřejmé, že pouze 5 stop pro rozlišení polohy je nedostačující (pouze 32 možných kombinací), z tohoto důvodu se používají snímače s vyšším počtem stop, např. 12, kdy rozlišení představuje 1/2¹² rozsahu (1/4096).

Snímač se zjednodušeně skládá z pevné a pohyblivé části. Podle konstrukce snímače, např. rotační snímač, může být nosič kódových stop pohyblivý a snímače stop (na obrázcích vyznačeny oranžovými body) jsou pevné. Při otáčení kotouče jedním nebo druhým směrem se mění stavy stop, které jsou zaznamenávány snímači jednotlivých stop. U konstrukce rotačních snímačů se vnější stopa využívá pro stavově nejnižší stopu (bit) z toho důvodu, že tato stopa má nejdelší obvod a je na ni možno umístit nejvyšší počet dělení (změn stavu) z hlediska technologie výroby snímače.

V elektrické podobě odpovídá průběh stavových signálů na jednotlivých stopách (bitech) stavu aktivace konkrétního snímače stopy, viz obrázek 8. Je-li kódování kotouče i pravítka logicky shodné, je shodný i průběh stavových signálů.

Obrázek 8
Průběh elektrických signálů jednotlivých stop